User login
Hospitals typically allocate beds based on historical patient volumes. If funding decreases, hospitals will usually try to maximize resource utilization by allocating beds to attain occupancies close to 100% for significant periods of time. This will invariably cause days in which hospital occupancy exceeds capacity, at which time critical entry points (such as the emergency department and operating room) will become blocked. This creates significant concerns over the patient quality of care.
Hospital administrators have very few options when hospital occupancy exceeds 100%. They could postpone admissions for “planned” cases, bring in additional staff to increase capacity, or instigate additional methods to increase hospital discharges such as expanding care resources in the community. All options are costly, bothersome, or cannot be actioned immediately. The need for these options could be minimized by enabling hospital administrators to make more informed decisions regarding hospital bed management by knowing the likely number of discharges in the next 24 hours.
Predicting the number of people who will be discharged in the next day can be approached in several ways. One approach would be to calculate each patient’s expected length of stay and then use the variation around that estimate to calculate each day’s discharge probability. Several studies have attempted to model hospital length of stay using a broad assortment of methodologies, but a mechanism to accurately predict this outcome has been elusive1,2 (with Verburg et al.3 concluding in their study’s abstract that “…it is difficult to predict length of stay…”). A second approach would be to use survival analysis methods to generate each patient’s hazard of discharge over time, which could be directly converted to an expected daily risk of discharge. However, this approach is complicated by the concurrent need to include time-dependent covariates and consider the competing risk of death in hospital, which can complicate survival modeling.4,5 A third approach would be the implementation of a longitudinal analysis using marginal models to predict the daily probability of discharge,6 but this method quickly overwhelms computer resources when large datasets are present.
In this study, we decided to use nonparametric models to predict the daily number of hospital discharges. We first identified patient groups with distinct discharge patterns. We then calculated the conditional daily discharge probability of patients in each of these groups. Finally, these conditional daily discharge probabilities were then summed for each hospital day to generate the expected number of discharges in the next 24 hours. This paper details the methods we used to create our model and the accuracy of its predictions.
METHODS
Study Setting and Databases Used for Analysis
The study took place at The Ottawa Hospital, a 1000-bed teaching hospital with 3 campuses that is the primary referral center in our region. The study was approved by our local research ethics board.
The Patient Registry Database records the date and time of admission for each patient (defined as the moment that a patient’s admission request is registered in the patient registration) and discharge (defined as the time when the patient’s discharge from hospital was entered into the patient registration) for hospital encounters. Emergency department encounters were also identified in the Patient Registry Database along with admission service, patient age and sex, and patient location throughout the admission. The Laboratory Database records all laboratory studies and results on all patients at the hospital.
Study Cohort
We used the Patient Registry Database to identify all people aged 1 year or more who were admitted to the hospital between January 1, 2013, and December 31, 2015. This time frame was selected to (i) ensure that data were complete; and (ii) complete calendar years of data were available for both derivation (patient-days in 2013-2014) and validation (2015) cohorts. Patients who were observed in the emergency room without admission to hospital were not included.
Study Outcome
The study outcome was the number of patients discharged from the hospital each day. For the analysis, the reference point for each day was 1 second past midnight; therefore, values for time-dependent covariates up to and including midnight were used to predict the number of discharges in the next 24 hours.
Study Covariates
Baseline (ie, time-independent) covariates included patient age and sex, admission service, hospital campus, whether or not the patient was admitted from the emergency department (all determined from the Patient Registry Database), and the Laboratory-based Acute Physiological Score (LAPS). The latter, which was calculated with the Laboratory Database using results for 14 tests (arterial pH, PaCO2, PaO2, anion gap, hematocrit, total white blood cell count, serum albumin, total bilirubin, creatinine, urea nitrogen, glucose, sodium, bicarbonate, and troponin I) measured in the 24-hour time frame preceding hospitalization, was derived by Escobar and colleagues7 to measure severity of illness and was subsequently validated in our hospital.8 The independent association of each laboratory perturbation with risk of death in hospital is reflected by the number of points assigned to each lab value with the total LAPS being the sum of these values. Time-dependent covariates included weekday in hospital and whether or not patients were in the intensive care unit.
Analysis
We used 3 stages to create a model to predict the daily expected number of discharges: we identified discharge risk strata containing patients having similar discharge patterns using data from patients in the derivation cohort (first stage); then, we generated the preliminary probability of discharge by determining the daily discharge probability in each discharge risk strata (second stage); finally, we modified the probability from the second stage based on the weekday and admission service and summed these probabilities to create the expected number of discharges on a particular date (third stage).
The first stage identified discharge risk strata based on the covariates listed above. This was determined by using a survival tree approach9 with proportional hazard regression models to generate the “splits.” These models were offered all covariates listed in the Study Covariates section. Admission service was clustered within 4 departments (obstetrics/gynecology, psychiatry, surgery, and medicine) and day of week was “binarized” into weekday/weekend-holiday (because the use of categorical variables with large numbers of groups can “stunt” regression trees due to small numbers of patients—and, therefore, statistical power—in each subgroup). The proportional hazards model identified the covariate having the strongest association with time to discharge (based on the Wald X2 value divided by the degrees of freedom). This variable was then used to split the cohort into subgroups (with continuous covariates being categorized into quartiles). The proportional hazards model was then repeated in each subgroup (with the previous splitting variable[s] excluded from the model). This process continued until no variable was associated with time to discharge with a P value less than .0001. This survival-tree was then used to cluster all patients into distinct discharge risk strata.
In the second stage, we generated the preliminary probability of discharge for a specific date. This was calculated by assigning all patients in hospital to their discharge risk strata (Appendix). We then measured the probability of discharge on each hospitalization day in all discharge risk strata using data from the previous 180 days (we only used the prior 180 days of data to account for temporal changes in hospital discharge patterns). For example, consider a 75-year-old patient on her third hospital day under obstetrics/gynecology on December 19, 2015 (a Saturday). This patient would be assigned to risk stratum #133 (Appendix A). We then measured the probability of discharge of all patients in this discharge risk stratum hospitalized in the previous 6 months (ie, between June 22, 2015, and December 18, 2015) on each hospital day. For risk stratum #133, the probability of discharge on hospital day 3 was 0.1111; therefore, our sample patient’s preliminary expected discharge probability was 0.1111.
To attain stable daily discharge probability estimates, a minimum of 50 patients per discharge risk stratum-hospitalization day combination was required. If there were less than 50 patients for a particular hospitalization day in a particular discharge risk stratum, we grouped hospitalization days in that risk stratum together until the minimum of 50 patients was collected.
The third (and final) stage accounted for the lack of granularity when we created the discharge risk strata in the first stage. As we mentioned above, admission service was clustered into 4 departments and the day of week was clustered into weekend/weekday. However, important variations in discharge probabilities could still exist within departments and between particular days of the week.10 Therefore, we created a correction factor to adjust the preliminary expected number of discharges based on the admission division and day of week. This correction factor used data from the 180 days prior to the analysis date within which the expected daily number of discharges was calculated (using the methods above). The correction factor was the relative difference between the observed and expected number of discharges within each division-day of week grouping.
For example, to calculate the correction factor for our sample patient presented above (75-year-old patient on hospital day 3 under gynecology on Saturday, December 19, 2015), we measured the observed number of discharges from gynecology on Saturdays between June 22, 2015, and December 18, 2015, (n = 206) and the expected number of discharges (n = 195.255) resulting in a correction factor of (observed-expected)/expected = (195.255-206)/195.206 = 0.05503. Therefore, the final expected discharge probability for our sample patient was 0.1111+0.1111*0.05503=0.1172. The expected number of discharges on a particular date was the preliminary expected number of discharges on that date (generated in the second stage) multiplied by the correction factor for the corresponding division-day or week group.
RESULTS
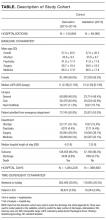
There were 192,859 admissions involving patients more than 1 year of age that spent at least part of their hospitalization between January 1, 2013, and December 31, 2015 (Table). Patients were middle-aged and slightly female predominant, with about half being admitted from the emergency department. Approximately 80% of admissions were to surgical or medical services. More than 95% of admissions ended with a discharge from the hospital with the remainder ending in a death. Almost 30% of hospitalization days occurred on weekends or holidays. Hospitalizations in the derivation (2013-2014) and validation (2015) group were essentially the same, except there was a slight drop in hospital length of stay (from a median of 4 days to 3 days) between the 2 periods.
Patient and hospital covariates importantly influenced the daily conditional probability of discharge (Figure 1). Patients admitted to the obstetrics/gynecology department were notably more likely to be discharged from hospital with no influence from the day of week. In contrast, the probability of discharge decreased notably on the weekends in the other departments. Patients on the ward were much more likely to be discharged than those in the intensive care unit, with increasing age associated with a decreased discharge likelihood in the former but not the latter patients. Finally, discharge probabilities varied only slightly between campuses at our hospital with discharge risk decreasing as severity of illness (as measured by LAPS) increased.
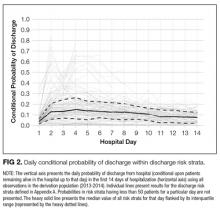
The TEND model contained 142 discharge risk strata (Appendix A). Weekend-holiday status had the strongest association with discharge probability (ie, it was the first splitting variable). The most complex discharge risk strata contained 6 covariates. The daily conditional probability of discharge during the first 2 weeks of hospitalization varied extensively between discharge risk strata (Figure 2). Overall, the conditional discharge probability increased from the first to the second day, remained relatively stable for several days, and then slowly decreased over time. However, this pattern and day-to-day variability differed extensively between risk strata.
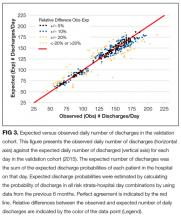
The observed daily number of discharges in the validation cohort varied extensively (median 139; interquartile range [IQR] 95-160; range 39-214). The TEND model accurately predicted the daily number of discharges with the expected daily number being strongly associated with the observed number (adjusted R2 = 89.2%; P < 0.0001; Figure 3). Calibration decreased but remained significant when we limited the analyses by hospital campus (General: R2 = 46.3%; P < 0.0001; Civic: R2 = 47.9%; P < 0.0001; Heart Institute: R2 = 18.1%; P < 0.0001). The expected number of daily discharges was an unbiased estimator of the observed number of discharges (its parameter estimate in a linear regression model with the observed number of discharges as the outcome variable was 1.0005; 95% confidence interval, 0.9647-1.0363). The absolute difference in the observed and expected daily number of discharges was small (median 1.6; IQR −6.8 to 9.4; range −37 to 63.4) as was the relative difference (median 1.4%; IQR −5.5% to 7.1%; range −40.9% to 43.4%). The expected number of discharges was within 20% of the observed number of discharges in 95.1% of days in 2015.
DISCUSSION
Knowing how many patients will soon be discharged from the hospital should greatly facilitate hospital planning. This study showed that the TEND model used simple patient and hospitalization covariates to accurately predict the number of patients who will be discharged from hospital in the next day.
We believe that this study has several notable findings. First, we think that using a nonparametric approach to predicting the daily number of discharges importantly increased accuracy. This approach allowed us to generate expected likelihoods based on actual discharge probabilities at our hospital in the most recent 6 months of hospitalization-days within patients having discharge patterns that were very similar to the patient in question (ie, discharge risk strata, Appendix A). This ensured that trends in hospitalization habits were accounted for without the need of a period variable in our model. In addition, the lack of parameters in the model will make it easier to transplant it to other hospitals. Second, we think that the accuracy of the predictions were remarkable given the relative “crudeness” of our predictors. By using relatively simple factors, the TEND model was able to output accurate predictions for the number of daily discharges (Figure 3).
This study joins several others that have attempted to accomplish the difficult task of predicting the number of hospital discharges by using digitized data. Barnes et al.11 created a model using regression random forest methods in a single medical service within a hospital to predict the daily number of discharges with impressive accuracy (mean daily number of discharges observed 8.29, expected 8.51). Interestingly, the model in this study was more accurate at predicting discharge likelihood than physicians. Levin et al.12 derived a model using discrete time logistic regression to predict the likelihood of discharge from a pediatric intensive care unit, finding that physician orders (captured via electronic order entry) could be categorized and used to significantly increase the accuracy of discharge likelihood. This study demonstrates the potential opportunities within health-related data from hospital data warehouses to improve prediction. We believe that continued work in this field will result in the increased use of digital data to help hospital administrators manage patient beds more efficiently and effectively than currently used resource intensive manual methods.13,14
Several issues should be kept in mind when interpreting our findings. First, our analysis is limited to a single institution in Canada. It will be important to determine if the TEND model methodology generalizes to other hospitals in different jurisdictions. Such an external validation, especially in multiple hospitals, will be important to show that the TEND model methodology works in other facilities. Hospitals could implement the TEND model if they are able to record daily values for each of the variables required to assign patients to a discharge risk stratum (Appendix A) and calculate within each the daily probability of discharge. Hospitals could derive their own discharge risk strata to account for covariates, which we did not include in our study but could be influential, such as insurance status. These discharge risk estimates could also be incorporated into the electronic medical record or hospital dashboards (as long as the data required to generate the estimates are available). These interventions would permit the expected number of hospital discharges (and even the patient-level probability of discharge) to be calculated on a daily basis. Second, 2 potential biases could have influenced the identification of our discharge risk strata (Appendix A). In this process, we used survival tree methods to separate patient-days into clusters having progressively more homogenous discharge patterns. Each split was determined by using a proportional hazards model that ignored the competing risks of death in hospital. In addition, the model expressed age and LAPS as continuous variables, whereas these covariates had to be categorized to create our risk strata groupings. The strength of a covariate’s association with an outcome will decrease when a continuous variable is categorized.15 Both of these issues might have biased our final risk strata categorization (Appendix A). Third, we limited our model to include simple covariates whose values could be determined relatively easily within most hospital administrative data systems. While this increases the generalizability to other hospital information systems, we believe that the introduction of other covariates to the model—such as daily vital signs, laboratory results, medications, or time from operations—could increase prediction accuracy. Finally, it is uncertain whether or not knowing the predicted number of discharges will improve the efficiency of bed management within the hospital. It seems logical that an accurate prediction of the number of beds that will be made available in the next day should improve decisions regarding the number of patients who could be admitted electively to the hospital. It remains to be seen, however, whether this truly happens.
In summary, we found that the TEND model used a handful of patient and hospitalization factors to accurately predict the expected number of discharges from hospital in the next day. Further work is required to implement this model into our institution’s data warehouse and then determine whether this prediction will improve the efficiency of bed management at our hospital.
Disclosure: CvW is supported by a University of Ottawa Department of Medicine Clinician Scientist Chair. The authors have no conflicts of interest
1. Austin PC, Rothwell DM, Tu JV. A comparison of statistical modeling strategies for analyzing length of stay after CABG surgery. Health Serv Outcomes Res Methodol. 2002;3:107-133.
2. Moran JL, Solomon PJ. A review of statistical estimators for risk-adjusted length of stay: analysis of the Australian and new Zealand intensive care adult patient data-base, 2008-2009. BMC Med Res Methodol. 2012;12:68. PubMed
3. Verburg IWM, de Keizer NF, de Jonge E, Peek N. Comparison of regression methods for modeling intensive care length of stay. PLoS One. 2014;9:e109684. PubMed
4. Beyersmann J, Schumacher M. Time-dependent covariates in the proportional subdistribution hazards model for competing risks. Biostatistics. 2008;9:765-776. PubMed
5. Latouche A, Porcher R, Chevret S. A note on including time-dependent covariate in regression model for competing risks data. Biom J. 2005;47:807-814. PubMed
6. Fitzmaurice GM, Laird NM, Ware JH. Marginal models: generalized estimating equations. Applied Longitudinal Analysis. 2nd ed. John Wiley & Sons; 2011;353-394.
7. Escobar GJ, Greene JD, Scheirer P, Gardner MN, Draper D, Kipnis P. Risk-adjusting hospital inpatient mortality using automated inpatient, outpatient, and laboratory databases. Med Care. 2008;46:232-239. PubMed
8. van Walraven C, Escobar GJ, Greene JD, Forster AJ. The Kaiser Permanente inpatient risk adjustment methodology was valid in an external patient population. J Clin Epidemiol. 2010;63:798-803. PubMed
9. Bou-Hamad I, Larocque D, Ben-Ameur H. A review of survival trees. Statist Surv. 2011;44-71.
10. van Walraven C, Bell CM. Risk of death or readmission among people discharged from hospital on Fridays. CMAJ. 2002;166:1672-1673. PubMed
11. Barnes S, Hamrock E, Toerper M, Siddiqui S, Levin S. Real-time prediction of inpatient length of stay for discharge prioritization. J Am Med Inform Assoc. 2016;23:e2-e10. PubMed
12. Levin SRP, Harley ETB, Fackler JCM, et al. Real-time forecasting of pediatric intensive care unit length of stay using computerized provider orders. Crit Care Med. 2012;40:3058-3064. PubMed
13. Resar R, Nolan K, Kaczynski D, Jensen K. Using real-time demand capacity management to improve hospitalwide patient flow. Jt Comm J Qual Patient Saf. 2011;37:217-227. PubMed
14. de Grood A, Blades K, Pendharkar SR. A review of discharge prediction processes in acute care hospitals. Healthc Policy. 2016;12:105-115. PubMed
15. van Walraven C, Hart RG. Leave ‘em alone - why continuous variables should be analyzed as such. Neuroepidemiology 2008;30:138-139. PubMed
Hospitals typically allocate beds based on historical patient volumes. If funding decreases, hospitals will usually try to maximize resource utilization by allocating beds to attain occupancies close to 100% for significant periods of time. This will invariably cause days in which hospital occupancy exceeds capacity, at which time critical entry points (such as the emergency department and operating room) will become blocked. This creates significant concerns over the patient quality of care.
Hospital administrators have very few options when hospital occupancy exceeds 100%. They could postpone admissions for “planned” cases, bring in additional staff to increase capacity, or instigate additional methods to increase hospital discharges such as expanding care resources in the community. All options are costly, bothersome, or cannot be actioned immediately. The need for these options could be minimized by enabling hospital administrators to make more informed decisions regarding hospital bed management by knowing the likely number of discharges in the next 24 hours.
Predicting the number of people who will be discharged in the next day can be approached in several ways. One approach would be to calculate each patient’s expected length of stay and then use the variation around that estimate to calculate each day’s discharge probability. Several studies have attempted to model hospital length of stay using a broad assortment of methodologies, but a mechanism to accurately predict this outcome has been elusive1,2 (with Verburg et al.3 concluding in their study’s abstract that “…it is difficult to predict length of stay…”). A second approach would be to use survival analysis methods to generate each patient’s hazard of discharge over time, which could be directly converted to an expected daily risk of discharge. However, this approach is complicated by the concurrent need to include time-dependent covariates and consider the competing risk of death in hospital, which can complicate survival modeling.4,5 A third approach would be the implementation of a longitudinal analysis using marginal models to predict the daily probability of discharge,6 but this method quickly overwhelms computer resources when large datasets are present.
In this study, we decided to use nonparametric models to predict the daily number of hospital discharges. We first identified patient groups with distinct discharge patterns. We then calculated the conditional daily discharge probability of patients in each of these groups. Finally, these conditional daily discharge probabilities were then summed for each hospital day to generate the expected number of discharges in the next 24 hours. This paper details the methods we used to create our model and the accuracy of its predictions.
METHODS
Study Setting and Databases Used for Analysis
The study took place at The Ottawa Hospital, a 1000-bed teaching hospital with 3 campuses that is the primary referral center in our region. The study was approved by our local research ethics board.
The Patient Registry Database records the date and time of admission for each patient (defined as the moment that a patient’s admission request is registered in the patient registration) and discharge (defined as the time when the patient’s discharge from hospital was entered into the patient registration) for hospital encounters. Emergency department encounters were also identified in the Patient Registry Database along with admission service, patient age and sex, and patient location throughout the admission. The Laboratory Database records all laboratory studies and results on all patients at the hospital.
Study Cohort
We used the Patient Registry Database to identify all people aged 1 year or more who were admitted to the hospital between January 1, 2013, and December 31, 2015. This time frame was selected to (i) ensure that data were complete; and (ii) complete calendar years of data were available for both derivation (patient-days in 2013-2014) and validation (2015) cohorts. Patients who were observed in the emergency room without admission to hospital were not included.
Study Outcome
The study outcome was the number of patients discharged from the hospital each day. For the analysis, the reference point for each day was 1 second past midnight; therefore, values for time-dependent covariates up to and including midnight were used to predict the number of discharges in the next 24 hours.
Study Covariates
Baseline (ie, time-independent) covariates included patient age and sex, admission service, hospital campus, whether or not the patient was admitted from the emergency department (all determined from the Patient Registry Database), and the Laboratory-based Acute Physiological Score (LAPS). The latter, which was calculated with the Laboratory Database using results for 14 tests (arterial pH, PaCO2, PaO2, anion gap, hematocrit, total white blood cell count, serum albumin, total bilirubin, creatinine, urea nitrogen, glucose, sodium, bicarbonate, and troponin I) measured in the 24-hour time frame preceding hospitalization, was derived by Escobar and colleagues7 to measure severity of illness and was subsequently validated in our hospital.8 The independent association of each laboratory perturbation with risk of death in hospital is reflected by the number of points assigned to each lab value with the total LAPS being the sum of these values. Time-dependent covariates included weekday in hospital and whether or not patients were in the intensive care unit.
Analysis
We used 3 stages to create a model to predict the daily expected number of discharges: we identified discharge risk strata containing patients having similar discharge patterns using data from patients in the derivation cohort (first stage); then, we generated the preliminary probability of discharge by determining the daily discharge probability in each discharge risk strata (second stage); finally, we modified the probability from the second stage based on the weekday and admission service and summed these probabilities to create the expected number of discharges on a particular date (third stage).
The first stage identified discharge risk strata based on the covariates listed above. This was determined by using a survival tree approach9 with proportional hazard regression models to generate the “splits.” These models were offered all covariates listed in the Study Covariates section. Admission service was clustered within 4 departments (obstetrics/gynecology, psychiatry, surgery, and medicine) and day of week was “binarized” into weekday/weekend-holiday (because the use of categorical variables with large numbers of groups can “stunt” regression trees due to small numbers of patients—and, therefore, statistical power—in each subgroup). The proportional hazards model identified the covariate having the strongest association with time to discharge (based on the Wald X2 value divided by the degrees of freedom). This variable was then used to split the cohort into subgroups (with continuous covariates being categorized into quartiles). The proportional hazards model was then repeated in each subgroup (with the previous splitting variable[s] excluded from the model). This process continued until no variable was associated with time to discharge with a P value less than .0001. This survival-tree was then used to cluster all patients into distinct discharge risk strata.
In the second stage, we generated the preliminary probability of discharge for a specific date. This was calculated by assigning all patients in hospital to their discharge risk strata (Appendix). We then measured the probability of discharge on each hospitalization day in all discharge risk strata using data from the previous 180 days (we only used the prior 180 days of data to account for temporal changes in hospital discharge patterns). For example, consider a 75-year-old patient on her third hospital day under obstetrics/gynecology on December 19, 2015 (a Saturday). This patient would be assigned to risk stratum #133 (Appendix A). We then measured the probability of discharge of all patients in this discharge risk stratum hospitalized in the previous 6 months (ie, between June 22, 2015, and December 18, 2015) on each hospital day. For risk stratum #133, the probability of discharge on hospital day 3 was 0.1111; therefore, our sample patient’s preliminary expected discharge probability was 0.1111.
To attain stable daily discharge probability estimates, a minimum of 50 patients per discharge risk stratum-hospitalization day combination was required. If there were less than 50 patients for a particular hospitalization day in a particular discharge risk stratum, we grouped hospitalization days in that risk stratum together until the minimum of 50 patients was collected.
The third (and final) stage accounted for the lack of granularity when we created the discharge risk strata in the first stage. As we mentioned above, admission service was clustered into 4 departments and the day of week was clustered into weekend/weekday. However, important variations in discharge probabilities could still exist within departments and between particular days of the week.10 Therefore, we created a correction factor to adjust the preliminary expected number of discharges based on the admission division and day of week. This correction factor used data from the 180 days prior to the analysis date within which the expected daily number of discharges was calculated (using the methods above). The correction factor was the relative difference between the observed and expected number of discharges within each division-day of week grouping.
For example, to calculate the correction factor for our sample patient presented above (75-year-old patient on hospital day 3 under gynecology on Saturday, December 19, 2015), we measured the observed number of discharges from gynecology on Saturdays between June 22, 2015, and December 18, 2015, (n = 206) and the expected number of discharges (n = 195.255) resulting in a correction factor of (observed-expected)/expected = (195.255-206)/195.206 = 0.05503. Therefore, the final expected discharge probability for our sample patient was 0.1111+0.1111*0.05503=0.1172. The expected number of discharges on a particular date was the preliminary expected number of discharges on that date (generated in the second stage) multiplied by the correction factor for the corresponding division-day or week group.
RESULTS
There were 192,859 admissions involving patients more than 1 year of age that spent at least part of their hospitalization between January 1, 2013, and December 31, 2015 (Table). Patients were middle-aged and slightly female predominant, with about half being admitted from the emergency department. Approximately 80% of admissions were to surgical or medical services. More than 95% of admissions ended with a discharge from the hospital with the remainder ending in a death. Almost 30% of hospitalization days occurred on weekends or holidays. Hospitalizations in the derivation (2013-2014) and validation (2015) group were essentially the same, except there was a slight drop in hospital length of stay (from a median of 4 days to 3 days) between the 2 periods.
Patient and hospital covariates importantly influenced the daily conditional probability of discharge (Figure 1). Patients admitted to the obstetrics/gynecology department were notably more likely to be discharged from hospital with no influence from the day of week. In contrast, the probability of discharge decreased notably on the weekends in the other departments. Patients on the ward were much more likely to be discharged than those in the intensive care unit, with increasing age associated with a decreased discharge likelihood in the former but not the latter patients. Finally, discharge probabilities varied only slightly between campuses at our hospital with discharge risk decreasing as severity of illness (as measured by LAPS) increased.
The TEND model contained 142 discharge risk strata (Appendix A). Weekend-holiday status had the strongest association with discharge probability (ie, it was the first splitting variable). The most complex discharge risk strata contained 6 covariates. The daily conditional probability of discharge during the first 2 weeks of hospitalization varied extensively between discharge risk strata (Figure 2). Overall, the conditional discharge probability increased from the first to the second day, remained relatively stable for several days, and then slowly decreased over time. However, this pattern and day-to-day variability differed extensively between risk strata.
The observed daily number of discharges in the validation cohort varied extensively (median 139; interquartile range [IQR] 95-160; range 39-214). The TEND model accurately predicted the daily number of discharges with the expected daily number being strongly associated with the observed number (adjusted R2 = 89.2%; P < 0.0001; Figure 3). Calibration decreased but remained significant when we limited the analyses by hospital campus (General: R2 = 46.3%; P < 0.0001; Civic: R2 = 47.9%; P < 0.0001; Heart Institute: R2 = 18.1%; P < 0.0001). The expected number of daily discharges was an unbiased estimator of the observed number of discharges (its parameter estimate in a linear regression model with the observed number of discharges as the outcome variable was 1.0005; 95% confidence interval, 0.9647-1.0363). The absolute difference in the observed and expected daily number of discharges was small (median 1.6; IQR −6.8 to 9.4; range −37 to 63.4) as was the relative difference (median 1.4%; IQR −5.5% to 7.1%; range −40.9% to 43.4%). The expected number of discharges was within 20% of the observed number of discharges in 95.1% of days in 2015.
DISCUSSION
Knowing how many patients will soon be discharged from the hospital should greatly facilitate hospital planning. This study showed that the TEND model used simple patient and hospitalization covariates to accurately predict the number of patients who will be discharged from hospital in the next day.
We believe that this study has several notable findings. First, we think that using a nonparametric approach to predicting the daily number of discharges importantly increased accuracy. This approach allowed us to generate expected likelihoods based on actual discharge probabilities at our hospital in the most recent 6 months of hospitalization-days within patients having discharge patterns that were very similar to the patient in question (ie, discharge risk strata, Appendix A). This ensured that trends in hospitalization habits were accounted for without the need of a period variable in our model. In addition, the lack of parameters in the model will make it easier to transplant it to other hospitals. Second, we think that the accuracy of the predictions were remarkable given the relative “crudeness” of our predictors. By using relatively simple factors, the TEND model was able to output accurate predictions for the number of daily discharges (Figure 3).
This study joins several others that have attempted to accomplish the difficult task of predicting the number of hospital discharges by using digitized data. Barnes et al.11 created a model using regression random forest methods in a single medical service within a hospital to predict the daily number of discharges with impressive accuracy (mean daily number of discharges observed 8.29, expected 8.51). Interestingly, the model in this study was more accurate at predicting discharge likelihood than physicians. Levin et al.12 derived a model using discrete time logistic regression to predict the likelihood of discharge from a pediatric intensive care unit, finding that physician orders (captured via electronic order entry) could be categorized and used to significantly increase the accuracy of discharge likelihood. This study demonstrates the potential opportunities within health-related data from hospital data warehouses to improve prediction. We believe that continued work in this field will result in the increased use of digital data to help hospital administrators manage patient beds more efficiently and effectively than currently used resource intensive manual methods.13,14
Several issues should be kept in mind when interpreting our findings. First, our analysis is limited to a single institution in Canada. It will be important to determine if the TEND model methodology generalizes to other hospitals in different jurisdictions. Such an external validation, especially in multiple hospitals, will be important to show that the TEND model methodology works in other facilities. Hospitals could implement the TEND model if they are able to record daily values for each of the variables required to assign patients to a discharge risk stratum (Appendix A) and calculate within each the daily probability of discharge. Hospitals could derive their own discharge risk strata to account for covariates, which we did not include in our study but could be influential, such as insurance status. These discharge risk estimates could also be incorporated into the electronic medical record or hospital dashboards (as long as the data required to generate the estimates are available). These interventions would permit the expected number of hospital discharges (and even the patient-level probability of discharge) to be calculated on a daily basis. Second, 2 potential biases could have influenced the identification of our discharge risk strata (Appendix A). In this process, we used survival tree methods to separate patient-days into clusters having progressively more homogenous discharge patterns. Each split was determined by using a proportional hazards model that ignored the competing risks of death in hospital. In addition, the model expressed age and LAPS as continuous variables, whereas these covariates had to be categorized to create our risk strata groupings. The strength of a covariate’s association with an outcome will decrease when a continuous variable is categorized.15 Both of these issues might have biased our final risk strata categorization (Appendix A). Third, we limited our model to include simple covariates whose values could be determined relatively easily within most hospital administrative data systems. While this increases the generalizability to other hospital information systems, we believe that the introduction of other covariates to the model—such as daily vital signs, laboratory results, medications, or time from operations—could increase prediction accuracy. Finally, it is uncertain whether or not knowing the predicted number of discharges will improve the efficiency of bed management within the hospital. It seems logical that an accurate prediction of the number of beds that will be made available in the next day should improve decisions regarding the number of patients who could be admitted electively to the hospital. It remains to be seen, however, whether this truly happens.
In summary, we found that the TEND model used a handful of patient and hospitalization factors to accurately predict the expected number of discharges from hospital in the next day. Further work is required to implement this model into our institution’s data warehouse and then determine whether this prediction will improve the efficiency of bed management at our hospital.
Disclosure: CvW is supported by a University of Ottawa Department of Medicine Clinician Scientist Chair. The authors have no conflicts of interest
Hospitals typically allocate beds based on historical patient volumes. If funding decreases, hospitals will usually try to maximize resource utilization by allocating beds to attain occupancies close to 100% for significant periods of time. This will invariably cause days in which hospital occupancy exceeds capacity, at which time critical entry points (such as the emergency department and operating room) will become blocked. This creates significant concerns over the patient quality of care.
Hospital administrators have very few options when hospital occupancy exceeds 100%. They could postpone admissions for “planned” cases, bring in additional staff to increase capacity, or instigate additional methods to increase hospital discharges such as expanding care resources in the community. All options are costly, bothersome, or cannot be actioned immediately. The need for these options could be minimized by enabling hospital administrators to make more informed decisions regarding hospital bed management by knowing the likely number of discharges in the next 24 hours.
Predicting the number of people who will be discharged in the next day can be approached in several ways. One approach would be to calculate each patient’s expected length of stay and then use the variation around that estimate to calculate each day’s discharge probability. Several studies have attempted to model hospital length of stay using a broad assortment of methodologies, but a mechanism to accurately predict this outcome has been elusive1,2 (with Verburg et al.3 concluding in their study’s abstract that “…it is difficult to predict length of stay…”). A second approach would be to use survival analysis methods to generate each patient’s hazard of discharge over time, which could be directly converted to an expected daily risk of discharge. However, this approach is complicated by the concurrent need to include time-dependent covariates and consider the competing risk of death in hospital, which can complicate survival modeling.4,5 A third approach would be the implementation of a longitudinal analysis using marginal models to predict the daily probability of discharge,6 but this method quickly overwhelms computer resources when large datasets are present.
In this study, we decided to use nonparametric models to predict the daily number of hospital discharges. We first identified patient groups with distinct discharge patterns. We then calculated the conditional daily discharge probability of patients in each of these groups. Finally, these conditional daily discharge probabilities were then summed for each hospital day to generate the expected number of discharges in the next 24 hours. This paper details the methods we used to create our model and the accuracy of its predictions.
METHODS
Study Setting and Databases Used for Analysis
The study took place at The Ottawa Hospital, a 1000-bed teaching hospital with 3 campuses that is the primary referral center in our region. The study was approved by our local research ethics board.
The Patient Registry Database records the date and time of admission for each patient (defined as the moment that a patient’s admission request is registered in the patient registration) and discharge (defined as the time when the patient’s discharge from hospital was entered into the patient registration) for hospital encounters. Emergency department encounters were also identified in the Patient Registry Database along with admission service, patient age and sex, and patient location throughout the admission. The Laboratory Database records all laboratory studies and results on all patients at the hospital.
Study Cohort
We used the Patient Registry Database to identify all people aged 1 year or more who were admitted to the hospital between January 1, 2013, and December 31, 2015. This time frame was selected to (i) ensure that data were complete; and (ii) complete calendar years of data were available for both derivation (patient-days in 2013-2014) and validation (2015) cohorts. Patients who were observed in the emergency room without admission to hospital were not included.
Study Outcome
The study outcome was the number of patients discharged from the hospital each day. For the analysis, the reference point for each day was 1 second past midnight; therefore, values for time-dependent covariates up to and including midnight were used to predict the number of discharges in the next 24 hours.
Study Covariates
Baseline (ie, time-independent) covariates included patient age and sex, admission service, hospital campus, whether or not the patient was admitted from the emergency department (all determined from the Patient Registry Database), and the Laboratory-based Acute Physiological Score (LAPS). The latter, which was calculated with the Laboratory Database using results for 14 tests (arterial pH, PaCO2, PaO2, anion gap, hematocrit, total white blood cell count, serum albumin, total bilirubin, creatinine, urea nitrogen, glucose, sodium, bicarbonate, and troponin I) measured in the 24-hour time frame preceding hospitalization, was derived by Escobar and colleagues7 to measure severity of illness and was subsequently validated in our hospital.8 The independent association of each laboratory perturbation with risk of death in hospital is reflected by the number of points assigned to each lab value with the total LAPS being the sum of these values. Time-dependent covariates included weekday in hospital and whether or not patients were in the intensive care unit.
Analysis
We used 3 stages to create a model to predict the daily expected number of discharges: we identified discharge risk strata containing patients having similar discharge patterns using data from patients in the derivation cohort (first stage); then, we generated the preliminary probability of discharge by determining the daily discharge probability in each discharge risk strata (second stage); finally, we modified the probability from the second stage based on the weekday and admission service and summed these probabilities to create the expected number of discharges on a particular date (third stage).
The first stage identified discharge risk strata based on the covariates listed above. This was determined by using a survival tree approach9 with proportional hazard regression models to generate the “splits.” These models were offered all covariates listed in the Study Covariates section. Admission service was clustered within 4 departments (obstetrics/gynecology, psychiatry, surgery, and medicine) and day of week was “binarized” into weekday/weekend-holiday (because the use of categorical variables with large numbers of groups can “stunt” regression trees due to small numbers of patients—and, therefore, statistical power—in each subgroup). The proportional hazards model identified the covariate having the strongest association with time to discharge (based on the Wald X2 value divided by the degrees of freedom). This variable was then used to split the cohort into subgroups (with continuous covariates being categorized into quartiles). The proportional hazards model was then repeated in each subgroup (with the previous splitting variable[s] excluded from the model). This process continued until no variable was associated with time to discharge with a P value less than .0001. This survival-tree was then used to cluster all patients into distinct discharge risk strata.
In the second stage, we generated the preliminary probability of discharge for a specific date. This was calculated by assigning all patients in hospital to their discharge risk strata (Appendix). We then measured the probability of discharge on each hospitalization day in all discharge risk strata using data from the previous 180 days (we only used the prior 180 days of data to account for temporal changes in hospital discharge patterns). For example, consider a 75-year-old patient on her third hospital day under obstetrics/gynecology on December 19, 2015 (a Saturday). This patient would be assigned to risk stratum #133 (Appendix A). We then measured the probability of discharge of all patients in this discharge risk stratum hospitalized in the previous 6 months (ie, between June 22, 2015, and December 18, 2015) on each hospital day. For risk stratum #133, the probability of discharge on hospital day 3 was 0.1111; therefore, our sample patient’s preliminary expected discharge probability was 0.1111.
To attain stable daily discharge probability estimates, a minimum of 50 patients per discharge risk stratum-hospitalization day combination was required. If there were less than 50 patients for a particular hospitalization day in a particular discharge risk stratum, we grouped hospitalization days in that risk stratum together until the minimum of 50 patients was collected.
The third (and final) stage accounted for the lack of granularity when we created the discharge risk strata in the first stage. As we mentioned above, admission service was clustered into 4 departments and the day of week was clustered into weekend/weekday. However, important variations in discharge probabilities could still exist within departments and between particular days of the week.10 Therefore, we created a correction factor to adjust the preliminary expected number of discharges based on the admission division and day of week. This correction factor used data from the 180 days prior to the analysis date within which the expected daily number of discharges was calculated (using the methods above). The correction factor was the relative difference between the observed and expected number of discharges within each division-day of week grouping.
For example, to calculate the correction factor for our sample patient presented above (75-year-old patient on hospital day 3 under gynecology on Saturday, December 19, 2015), we measured the observed number of discharges from gynecology on Saturdays between June 22, 2015, and December 18, 2015, (n = 206) and the expected number of discharges (n = 195.255) resulting in a correction factor of (observed-expected)/expected = (195.255-206)/195.206 = 0.05503. Therefore, the final expected discharge probability for our sample patient was 0.1111+0.1111*0.05503=0.1172. The expected number of discharges on a particular date was the preliminary expected number of discharges on that date (generated in the second stage) multiplied by the correction factor for the corresponding division-day or week group.
RESULTS
There were 192,859 admissions involving patients more than 1 year of age that spent at least part of their hospitalization between January 1, 2013, and December 31, 2015 (Table). Patients were middle-aged and slightly female predominant, with about half being admitted from the emergency department. Approximately 80% of admissions were to surgical or medical services. More than 95% of admissions ended with a discharge from the hospital with the remainder ending in a death. Almost 30% of hospitalization days occurred on weekends or holidays. Hospitalizations in the derivation (2013-2014) and validation (2015) group were essentially the same, except there was a slight drop in hospital length of stay (from a median of 4 days to 3 days) between the 2 periods.
Patient and hospital covariates importantly influenced the daily conditional probability of discharge (Figure 1). Patients admitted to the obstetrics/gynecology department were notably more likely to be discharged from hospital with no influence from the day of week. In contrast, the probability of discharge decreased notably on the weekends in the other departments. Patients on the ward were much more likely to be discharged than those in the intensive care unit, with increasing age associated with a decreased discharge likelihood in the former but not the latter patients. Finally, discharge probabilities varied only slightly between campuses at our hospital with discharge risk decreasing as severity of illness (as measured by LAPS) increased.
The TEND model contained 142 discharge risk strata (Appendix A). Weekend-holiday status had the strongest association with discharge probability (ie, it was the first splitting variable). The most complex discharge risk strata contained 6 covariates. The daily conditional probability of discharge during the first 2 weeks of hospitalization varied extensively between discharge risk strata (Figure 2). Overall, the conditional discharge probability increased from the first to the second day, remained relatively stable for several days, and then slowly decreased over time. However, this pattern and day-to-day variability differed extensively between risk strata.
The observed daily number of discharges in the validation cohort varied extensively (median 139; interquartile range [IQR] 95-160; range 39-214). The TEND model accurately predicted the daily number of discharges with the expected daily number being strongly associated with the observed number (adjusted R2 = 89.2%; P < 0.0001; Figure 3). Calibration decreased but remained significant when we limited the analyses by hospital campus (General: R2 = 46.3%; P < 0.0001; Civic: R2 = 47.9%; P < 0.0001; Heart Institute: R2 = 18.1%; P < 0.0001). The expected number of daily discharges was an unbiased estimator of the observed number of discharges (its parameter estimate in a linear regression model with the observed number of discharges as the outcome variable was 1.0005; 95% confidence interval, 0.9647-1.0363). The absolute difference in the observed and expected daily number of discharges was small (median 1.6; IQR −6.8 to 9.4; range −37 to 63.4) as was the relative difference (median 1.4%; IQR −5.5% to 7.1%; range −40.9% to 43.4%). The expected number of discharges was within 20% of the observed number of discharges in 95.1% of days in 2015.
DISCUSSION
Knowing how many patients will soon be discharged from the hospital should greatly facilitate hospital planning. This study showed that the TEND model used simple patient and hospitalization covariates to accurately predict the number of patients who will be discharged from hospital in the next day.
We believe that this study has several notable findings. First, we think that using a nonparametric approach to predicting the daily number of discharges importantly increased accuracy. This approach allowed us to generate expected likelihoods based on actual discharge probabilities at our hospital in the most recent 6 months of hospitalization-days within patients having discharge patterns that were very similar to the patient in question (ie, discharge risk strata, Appendix A). This ensured that trends in hospitalization habits were accounted for without the need of a period variable in our model. In addition, the lack of parameters in the model will make it easier to transplant it to other hospitals. Second, we think that the accuracy of the predictions were remarkable given the relative “crudeness” of our predictors. By using relatively simple factors, the TEND model was able to output accurate predictions for the number of daily discharges (Figure 3).
This study joins several others that have attempted to accomplish the difficult task of predicting the number of hospital discharges by using digitized data. Barnes et al.11 created a model using regression random forest methods in a single medical service within a hospital to predict the daily number of discharges with impressive accuracy (mean daily number of discharges observed 8.29, expected 8.51). Interestingly, the model in this study was more accurate at predicting discharge likelihood than physicians. Levin et al.12 derived a model using discrete time logistic regression to predict the likelihood of discharge from a pediatric intensive care unit, finding that physician orders (captured via electronic order entry) could be categorized and used to significantly increase the accuracy of discharge likelihood. This study demonstrates the potential opportunities within health-related data from hospital data warehouses to improve prediction. We believe that continued work in this field will result in the increased use of digital data to help hospital administrators manage patient beds more efficiently and effectively than currently used resource intensive manual methods.13,14
Several issues should be kept in mind when interpreting our findings. First, our analysis is limited to a single institution in Canada. It will be important to determine if the TEND model methodology generalizes to other hospitals in different jurisdictions. Such an external validation, especially in multiple hospitals, will be important to show that the TEND model methodology works in other facilities. Hospitals could implement the TEND model if they are able to record daily values for each of the variables required to assign patients to a discharge risk stratum (Appendix A) and calculate within each the daily probability of discharge. Hospitals could derive their own discharge risk strata to account for covariates, which we did not include in our study but could be influential, such as insurance status. These discharge risk estimates could also be incorporated into the electronic medical record or hospital dashboards (as long as the data required to generate the estimates are available). These interventions would permit the expected number of hospital discharges (and even the patient-level probability of discharge) to be calculated on a daily basis. Second, 2 potential biases could have influenced the identification of our discharge risk strata (Appendix A). In this process, we used survival tree methods to separate patient-days into clusters having progressively more homogenous discharge patterns. Each split was determined by using a proportional hazards model that ignored the competing risks of death in hospital. In addition, the model expressed age and LAPS as continuous variables, whereas these covariates had to be categorized to create our risk strata groupings. The strength of a covariate’s association with an outcome will decrease when a continuous variable is categorized.15 Both of these issues might have biased our final risk strata categorization (Appendix A). Third, we limited our model to include simple covariates whose values could be determined relatively easily within most hospital administrative data systems. While this increases the generalizability to other hospital information systems, we believe that the introduction of other covariates to the model—such as daily vital signs, laboratory results, medications, or time from operations—could increase prediction accuracy. Finally, it is uncertain whether or not knowing the predicted number of discharges will improve the efficiency of bed management within the hospital. It seems logical that an accurate prediction of the number of beds that will be made available in the next day should improve decisions regarding the number of patients who could be admitted electively to the hospital. It remains to be seen, however, whether this truly happens.
In summary, we found that the TEND model used a handful of patient and hospitalization factors to accurately predict the expected number of discharges from hospital in the next day. Further work is required to implement this model into our institution’s data warehouse and then determine whether this prediction will improve the efficiency of bed management at our hospital.
Disclosure: CvW is supported by a University of Ottawa Department of Medicine Clinician Scientist Chair. The authors have no conflicts of interest
1. Austin PC, Rothwell DM, Tu JV. A comparison of statistical modeling strategies for analyzing length of stay after CABG surgery. Health Serv Outcomes Res Methodol. 2002;3:107-133.
2. Moran JL, Solomon PJ. A review of statistical estimators for risk-adjusted length of stay: analysis of the Australian and new Zealand intensive care adult patient data-base, 2008-2009. BMC Med Res Methodol. 2012;12:68. PubMed
3. Verburg IWM, de Keizer NF, de Jonge E, Peek N. Comparison of regression methods for modeling intensive care length of stay. PLoS One. 2014;9:e109684. PubMed
4. Beyersmann J, Schumacher M. Time-dependent covariates in the proportional subdistribution hazards model for competing risks. Biostatistics. 2008;9:765-776. PubMed
5. Latouche A, Porcher R, Chevret S. A note on including time-dependent covariate in regression model for competing risks data. Biom J. 2005;47:807-814. PubMed
6. Fitzmaurice GM, Laird NM, Ware JH. Marginal models: generalized estimating equations. Applied Longitudinal Analysis. 2nd ed. John Wiley & Sons; 2011;353-394.
7. Escobar GJ, Greene JD, Scheirer P, Gardner MN, Draper D, Kipnis P. Risk-adjusting hospital inpatient mortality using automated inpatient, outpatient, and laboratory databases. Med Care. 2008;46:232-239. PubMed
8. van Walraven C, Escobar GJ, Greene JD, Forster AJ. The Kaiser Permanente inpatient risk adjustment methodology was valid in an external patient population. J Clin Epidemiol. 2010;63:798-803. PubMed
9. Bou-Hamad I, Larocque D, Ben-Ameur H. A review of survival trees. Statist Surv. 2011;44-71.
10. van Walraven C, Bell CM. Risk of death or readmission among people discharged from hospital on Fridays. CMAJ. 2002;166:1672-1673. PubMed
11. Barnes S, Hamrock E, Toerper M, Siddiqui S, Levin S. Real-time prediction of inpatient length of stay for discharge prioritization. J Am Med Inform Assoc. 2016;23:e2-e10. PubMed
12. Levin SRP, Harley ETB, Fackler JCM, et al. Real-time forecasting of pediatric intensive care unit length of stay using computerized provider orders. Crit Care Med. 2012;40:3058-3064. PubMed
13. Resar R, Nolan K, Kaczynski D, Jensen K. Using real-time demand capacity management to improve hospitalwide patient flow. Jt Comm J Qual Patient Saf. 2011;37:217-227. PubMed
14. de Grood A, Blades K, Pendharkar SR. A review of discharge prediction processes in acute care hospitals. Healthc Policy. 2016;12:105-115. PubMed
15. van Walraven C, Hart RG. Leave ‘em alone - why continuous variables should be analyzed as such. Neuroepidemiology 2008;30:138-139. PubMed
1. Austin PC, Rothwell DM, Tu JV. A comparison of statistical modeling strategies for analyzing length of stay after CABG surgery. Health Serv Outcomes Res Methodol. 2002;3:107-133.
2. Moran JL, Solomon PJ. A review of statistical estimators for risk-adjusted length of stay: analysis of the Australian and new Zealand intensive care adult patient data-base, 2008-2009. BMC Med Res Methodol. 2012;12:68. PubMed
3. Verburg IWM, de Keizer NF, de Jonge E, Peek N. Comparison of regression methods for modeling intensive care length of stay. PLoS One. 2014;9:e109684. PubMed
4. Beyersmann J, Schumacher M. Time-dependent covariates in the proportional subdistribution hazards model for competing risks. Biostatistics. 2008;9:765-776. PubMed
5. Latouche A, Porcher R, Chevret S. A note on including time-dependent covariate in regression model for competing risks data. Biom J. 2005;47:807-814. PubMed
6. Fitzmaurice GM, Laird NM, Ware JH. Marginal models: generalized estimating equations. Applied Longitudinal Analysis. 2nd ed. John Wiley & Sons; 2011;353-394.
7. Escobar GJ, Greene JD, Scheirer P, Gardner MN, Draper D, Kipnis P. Risk-adjusting hospital inpatient mortality using automated inpatient, outpatient, and laboratory databases. Med Care. 2008;46:232-239. PubMed
8. van Walraven C, Escobar GJ, Greene JD, Forster AJ. The Kaiser Permanente inpatient risk adjustment methodology was valid in an external patient population. J Clin Epidemiol. 2010;63:798-803. PubMed
9. Bou-Hamad I, Larocque D, Ben-Ameur H. A review of survival trees. Statist Surv. 2011;44-71.
10. van Walraven C, Bell CM. Risk of death or readmission among people discharged from hospital on Fridays. CMAJ. 2002;166:1672-1673. PubMed
11. Barnes S, Hamrock E, Toerper M, Siddiqui S, Levin S. Real-time prediction of inpatient length of stay for discharge prioritization. J Am Med Inform Assoc. 2016;23:e2-e10. PubMed
12. Levin SRP, Harley ETB, Fackler JCM, et al. Real-time forecasting of pediatric intensive care unit length of stay using computerized provider orders. Crit Care Med. 2012;40:3058-3064. PubMed
13. Resar R, Nolan K, Kaczynski D, Jensen K. Using real-time demand capacity management to improve hospitalwide patient flow. Jt Comm J Qual Patient Saf. 2011;37:217-227. PubMed
14. de Grood A, Blades K, Pendharkar SR. A review of discharge prediction processes in acute care hospitals. Healthc Policy. 2016;12:105-115. PubMed
15. van Walraven C, Hart RG. Leave ‘em alone - why continuous variables should be analyzed as such. Neuroepidemiology 2008;30:138-139. PubMed
© 2018 Society of Hospital Medicine